- Accueil
- Les suites
- Les fonctions
- Fonctions trigonométriques
- Fonction exponentielle
- Les nombres complexes
- Probabilités
- Logarithme népérien
- Primitives et intégration
- Lois continues
- Géométrie dans l'espace
- Lois normales (avec échantillonnage)
- R.O.C
- Exercices de bac
- Exercices à prise d'initiatives
- Bac 2015
- Rappels
- Contactez-moi
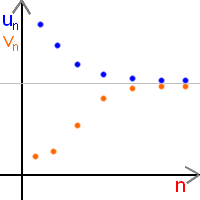
Suites adjacentes
Deux suites et
sont dites adjacentes si :
-
est croissante
-
est décroissante
Posons la suite auxiliaire définie sur
par :
. On sait que :
est croissante et
est décroissante. Étudions le signe de
.
Or, d'après les définitions : et
. Par conséquent :
.
Donc la suite
est croissante.
Ainsi, d'après le théorème, puisque la suite est croissante et converge vers un réel, alors on a, dans ce cas : . Ainsi, on a :
Maintenant, toujours d'après les définitions, on a : . La suite
est croissante et majorée par
, donc elle est converge. Idem pour la suite
qui elle, est décroissante et minorée par
.
Ainsi, on peut dire :
Par addition (), on a :
Or on sait que :
Par conséquent, on a : , les deux suites convergent vers la même limite.
Exemple : considérons la suite définie sur
par :
., et la suite
définie sur
par :
. Les
deux suites sont adjacentes.
Voir image ci-dessous pour se faire une idée de la représentation de deux suites adjacentes.